Aso (remote), Komori (remote), Takano
Abstract
Calibration of the error signal of OMC length control is ongoing. First the actuator efficiency was calibrated, and we got almost the same value as this report. Next step is to calibrate the error signal from the transfer function measurement from the actuator input to the error signal.
Detail
To discuss the effect of the vibration to the fluctuation of OMC length quantitatively, we started to calibrate the error signal of OMC length.
We came up two strategies:
Aso method
- Calibrate the actuator efficiency of the piezo [m/cnt] by scanning the cavity length and measuring the counts which is necessary to change the length by 1 FSR of the cavity.
- Add an offset to the input (K1:OMC-LSC_ERR_OFFSET) to detune the cavity.
- Check the change of the actuator input (K1:OMC-PZT_HV1_OUT). With the actuator efficiency we estimated above, we know how much the actuator moves.
- Check the change of the error signal (K1:OMC-LSC_ERR_IN1). It should be a value that is the same as the offset we added with an opposite sign.
- Comparing the values obtained in 3 and 4, we get the calibration factor of the error signal [m/cnt]
Komori method
- Calibrate the actuator efficiency of the piezo [m/cnt] by scanning the cavity length and measuring the counts which is necessary to change the length by 1 FSR of the cavity (same as the previous one).
- Inject an excitation to the actuator input (K1:OMC-PZT_HV1_EXC) and measure the transfer function to the error signal (K1:OMC-LSC_ERR_IN1).
- The transfer function is given by
, where
[m/cnt] is the actuator efficiency,
[m/cnt] is the calibration factor, and
[cnt/cnt] is the feedback filter. We already know
and
, then we get
.
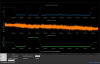
First of all, I measured the actuator efficiency by scanning the cavity. Figure1 shows the timeseries of the scan. The distance between the peaks are not the same, because of the nonlinearity and the hysterisis of the piezo actuator. To avoid these effects, I picked up the peaks at which the actuator input is avobe 3000 cnt. Finally, we get the actuator efficiency of 1.3(1)e-10 [m/cnt], which is consistent with the previous measurement.
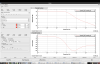
Next, I tried adding offsets and checking the shift of the error and the feedback signal. Figure2 shows the timeseries when I changed the offset of the error signal. It seems that the shift of the feedback signal is buried with the background fluctuation. I could not add larger offset because the cavity lock was lost, so I gave up this method.
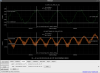
I moved on to the Komori method. I injected an excitation to K1:OMC-PZT_HV1_EXC and measured the transfer functions between many channels. Figure3 shows the measured results. The plots in the left column are the open loop transfer function. In the current control setup UGF is around 20 Hz. The plots in the right column are the transfer functions from the excitation signal (K1:OMC-PZT_HV1_EXC) to the error signal (K1:OMC-LSC_ERR_IN1/OUT). Above UGF, they should be approximated to , and from the measurement it seems to have some frequency dependency. Considering the circuit diagram of the piezo driver (here), there is a pole at 6.4 Hz in the driver and this can explain the frequency dependency above UGF.
Now we have enough data to estimate the calibration factor of the error signal. We will report the results later.