Federico, Irene, Eleonora, Washimi, TTanaka
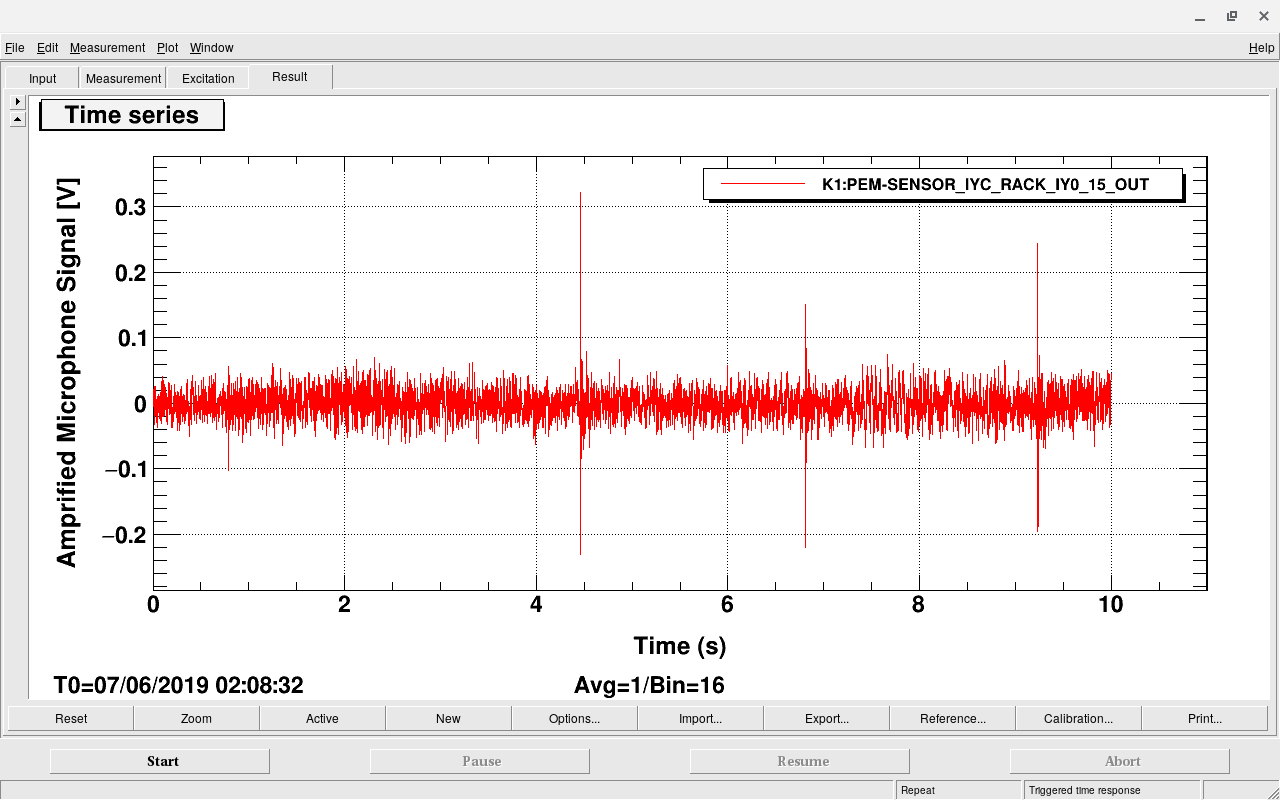
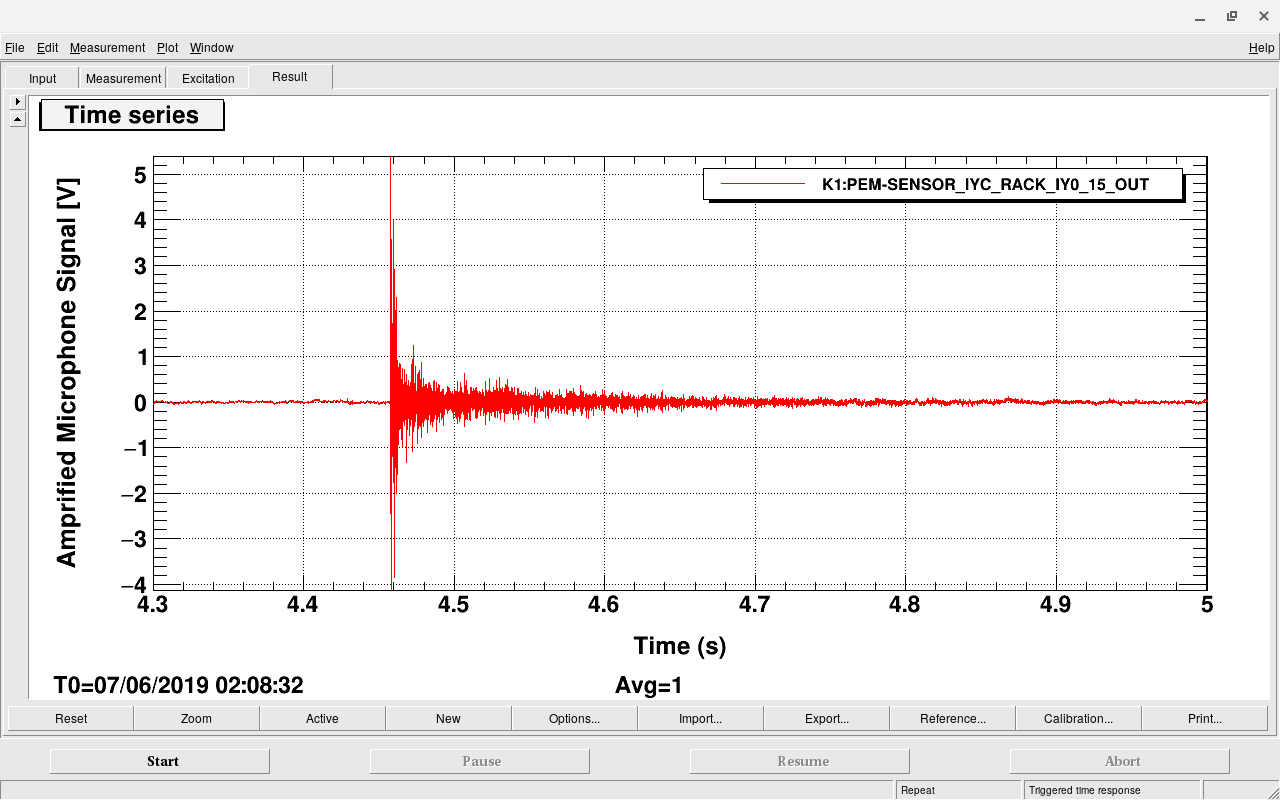
We performed acoustic injection to measure the echo at the center area.
We outputted whitening sound around 10:30-50 and turned off some machines (below) around 10:26-11:21.
Federico, Irene, Eleonora, Washimi, TTanaka
We performed acoustic injection to measure the echo at the center area.
We outputted whitening sound around 10:30-50 and turned off some machines (below) around 10:26-11:21.
I update my analysis. (Previous result, already reported, is JGW-L1910221-v1)
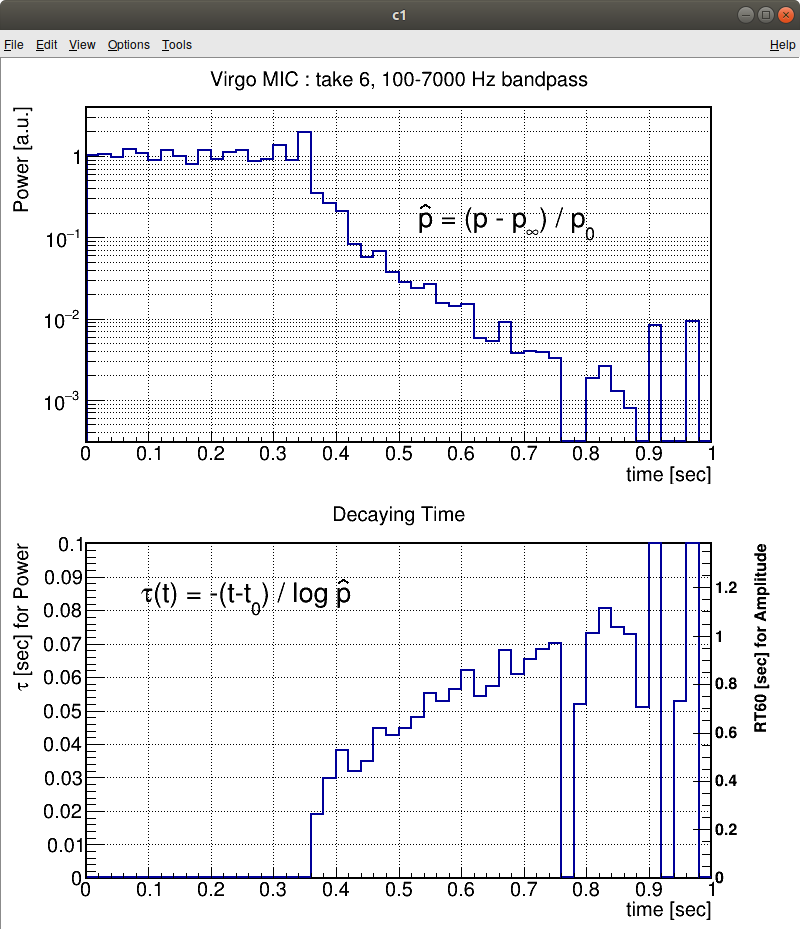
To obtain the frequency dependence of decaing time, I select the region of
Their shapes are not simple exponentioal yet.
But to compair them by eye, decaying time is increasing as the frequency.
I perform fitting to the RMS timeseries, and obtain the RT60 value. (see attachments)
The results are
In these bins, the center value and error is obtained by TH1::GetStdDev() / TH1::GetStdDevError() in ROOT 6.
But these errors look too small
The shape of RMS time series has some periodic structure due to the bandpass filter.
This is reason why the deviation between bins were larger than StdDevError in my previous k-log.
So, I try to evaluate the decaying time by power integral instead of RMS.
For each 0.02 sec, generate the power spectrum dencity and integral it within a frequency region.
I performed this procedure for 3 regions, 100-500 Hz, 1-3 kHz, and 5-7kHz. (attached plot)
In this plot, significant dependence of frequency is not seen.
To evaluate the non-constant dacaying time, I apry the method used in scintillation detector.
For the time series of a normalized power
we can calicurate tau as
The result is here,
Yesterday (2019/6/7), I tried the followup measurement of the accuostic reverberation time in the corner area.
I used the starter for sports (JGW-S1910280).

I used diaggui for data taking, instead of changing the DQ rate.