We updated calibration parameters as follows.
DARM parameters will be also measured tomorrow again for the final confirmation.
Unknown phase delay can be seen.
We need to identify that they comes from sensing or actuation for providing offline h(t).
We also updated the EPICS records of the transfer function model at line frequency
which were listed in JGW-L2314962.
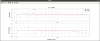
DARM (Fig.1-2)
EX_IM: -1.3876e-14 => -1.4188e-14
EX_TM: -3.5241e-14 => -3.4567e-14
H_DARM: 253.921dB -> 254.020dB
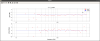
MICH (Fig.3-4)
BS_TM: 5.9e-11 => 6.0392e-11
H_MICH: 174.815dB => 175.958dB
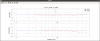
PRCL (Fig.5-6)
PRM_TM: -7.0e-12(-223.149,"dB) => -8.8179e-10
H_PRCL: 184.855dB => 182.998dB
I checked a breakdown of unknown phase delay in DARM loop (~4deg@500Hz)
For this purpose, residuals of measured actuation function, A, and sensing function, C, with their model were evaluated.
Measured A (Fig.1) and C (Fig.2) were evaluated as
A = [DARM1_IN1/TM_CAL_EXC] / [DARM1_IN1/RxPD] * P_model
= [AC/(1+G)] / [PC/(1+G)] * P_model
and
C = [DARM1_IN1/RxPD] / [DARM1_IN2/DARM1_EXC] / P_model
= [PC/(1+G)] / [1/(1+G)] / P_model,
respectively.
Residuals of these TFs and their models are shown in Fig.3 (Actuation, A) and Fig.4 (Sensing, C).
Because of the statistical fluctuation, it's not clear that the existence of the phase delay in both TFs.
But by computing A * C (multiplication of the data point in Fig3 and Fig.4),
it can be seen more clear as shown in Fig.5 and Fig.6.
This fact suggest the unknown phase delay comes from the actuation function of A, or the sensing function of C, not a digital servo, D.
And also, we cannot see the residual in the gain of TF.
So I searched best fit value of additional time delay of A and C.
At this time, measurement points at which coherence is too bad (below 30Hz) are removed from fitting.
Fitting results for actuation function and sensing function is shown in Fig.7 and Fig.8.
According to these results, most of time delay should be assigned in actuation function (unit of p0 is usec).
An additional 22us delay in actuation function is consistent with the phase delay in DARM loop (4deg@500Hz).
From these results, I concluded the unknown phase delay should be assigned in the actuation function, A.