KAGRA Logbook

VIS (General)

masahide.tamaki - 16:59 Monday 10 October 2022 (22429)

Suspension control noise projection (ETMY_MN_L and BS_TM_L)

Summary

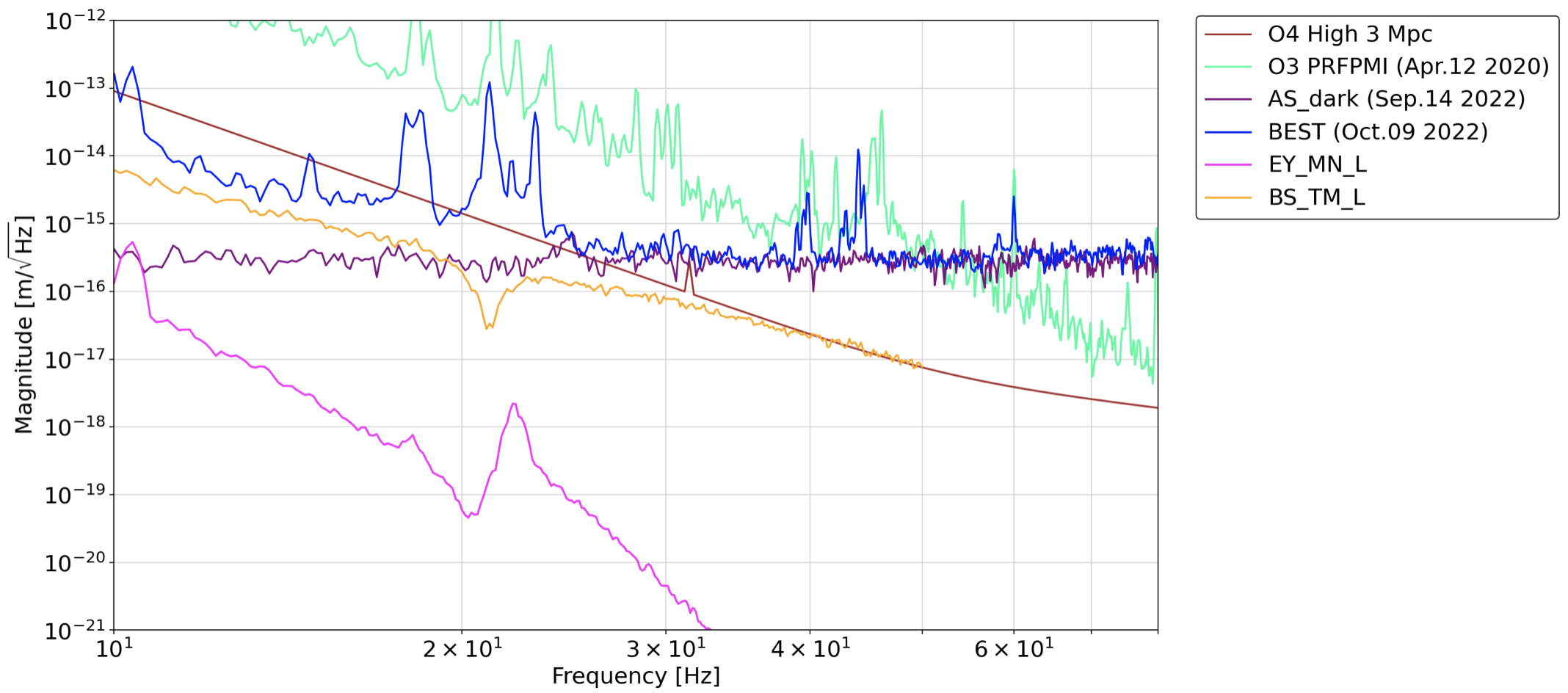
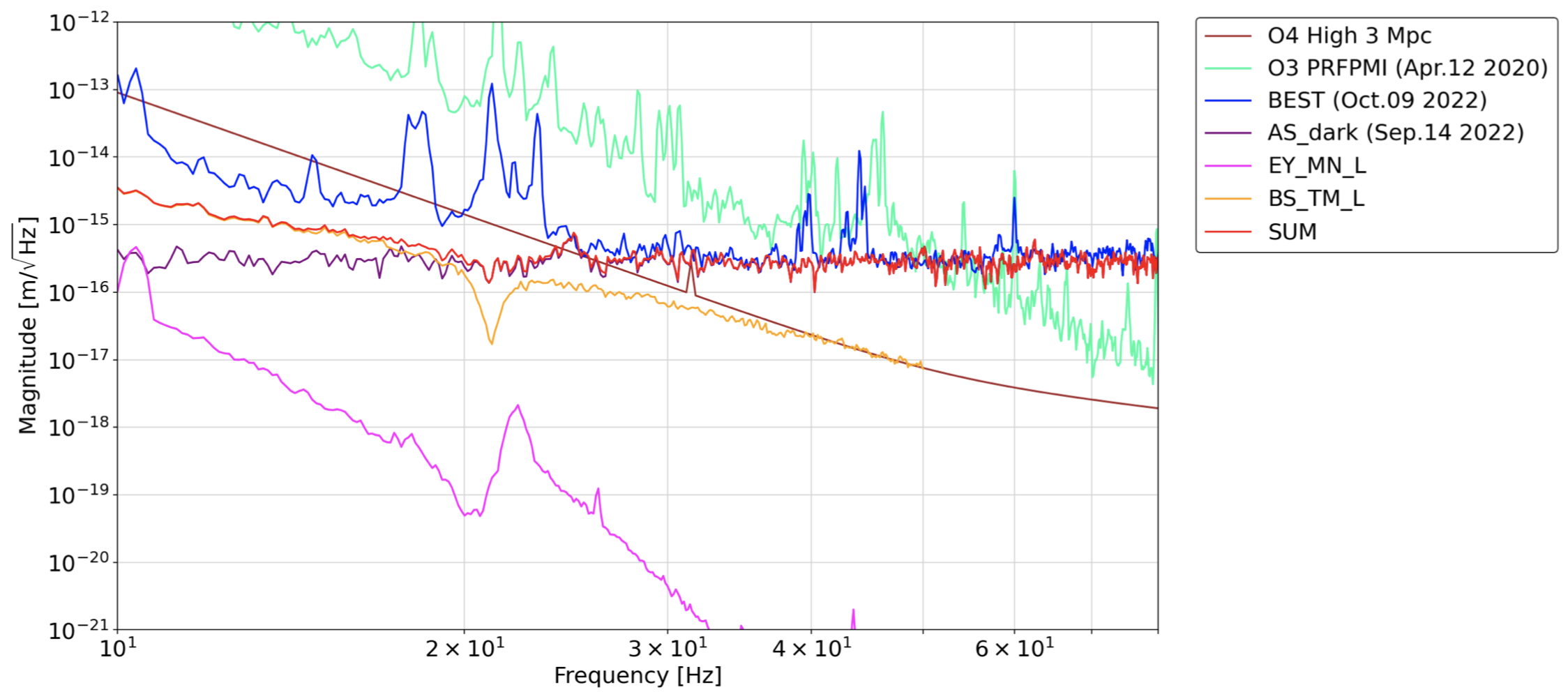
Using the TFs (from EY_MN_L to DARM and from BS_TM_L to DARM) measured by Ushiba-san (klog22367 and klog22415), I calculated suspension control noise contribution to DARM.
The calculations have been done only for these two so far, but anyway, the results are as follows (Fig1&2).

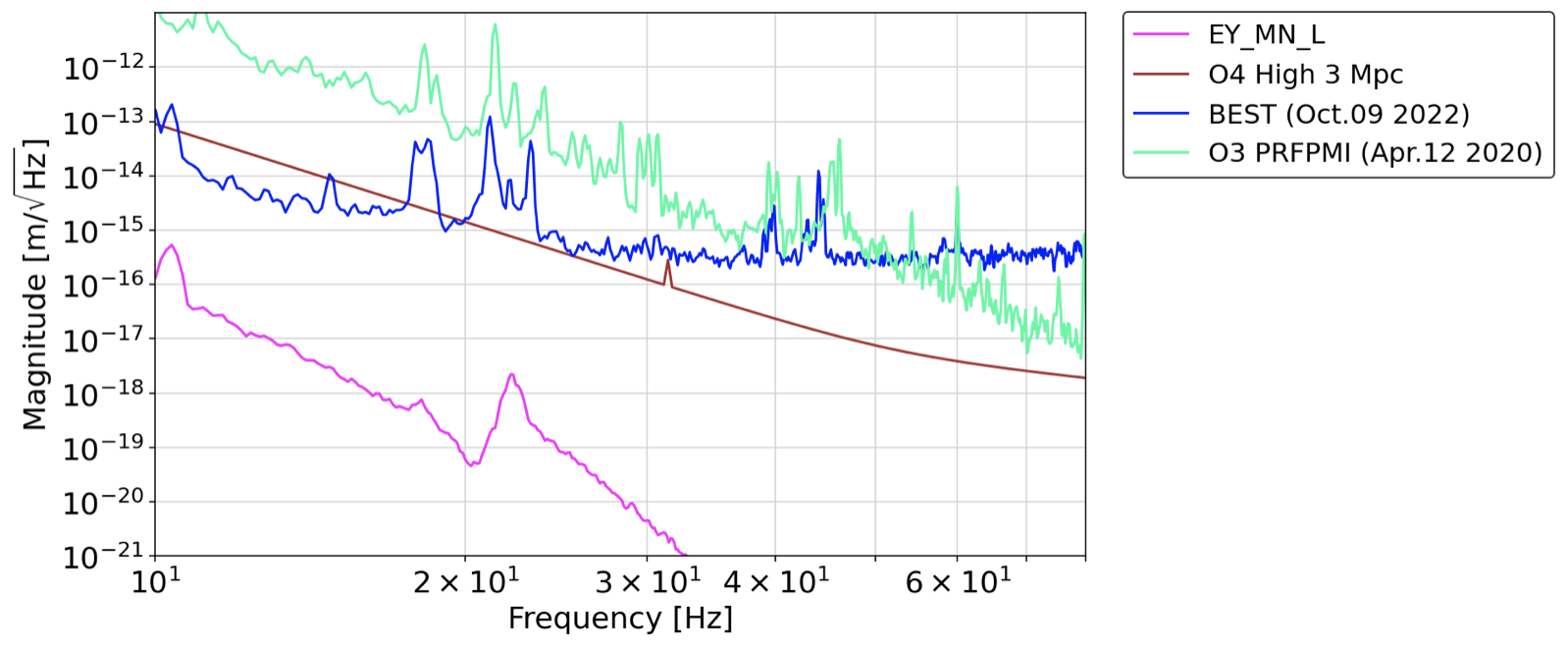
Fig1 EY_MN_L

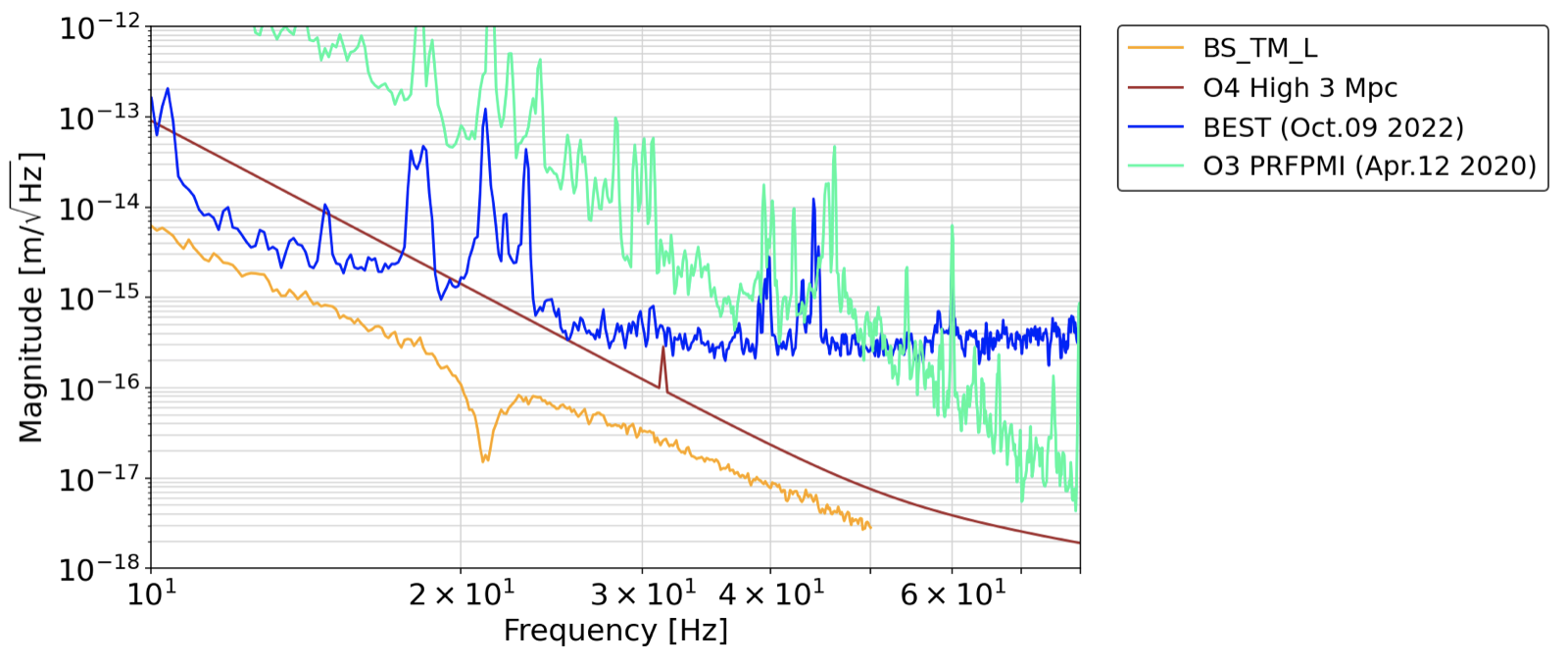
Fig2 BS_TM_L

We can say the control noise of EY_MN_L and BS_TM_L is sufficiently small for the 3-Mpc sensitivity curve.
♦ For more information on sensitivity curve, please see klog22422.

I am currently optimising the control of other suspensions or DoFs, so as soon as that is finished I will measure the transfer function and spectrum and will calculate the noise projection.

Supplement

► TF from EY_MN_L to DARM (10-80 Hz) is Fig3 and TF from BS_TM_L to DARM (10-50 Hz) is Fig4.

► Spectrum of ETMY_MN_DAMP_L_OUT_DQ is Fig5 and Spectrum of BS_TM_SUMOUT_L_OUT_DQ is Fig6.

► Control noise projection = TF × spectrum of SUS_STAGE_DoF
♦ I have given linear interpolation to the TFs with Scipy.interpolate (Fig7&8).
♦ This projection doesn't include DAC noise ---- NOT TF × sqrt(spectrum of SUS_STAGE_DoF**2 + DAC noise**2)

Images attached to this report

Comments to this report:

masahide.tamaki - 23:21 Tuesday 11 October 2022 (22447)

I found a mistake in calibration on BS_TM_L control noise contribution.
The correct results are shown in the figure below.

Images attached to this comment

tomotada.akutsu - 23:55 Tuesday 11 October 2022 (22448)

I see, interesting. Why don't you also make some additional calculation a little? like taking a root-mean square sum of the BS noise contribution and AS dark noise contribution, and compare this sum with the DARM??

masahide.tamaki - 12:31 Wednesday 12 October 2022 (22449)

Thank you for your comment.

I added a root-mean square sum (red line).
For now, sqrt(AS dark**2 + EY_MN_L**2 + BS_TM_L**2).

I have not yet calculated the noise of the other suspensions and degrees of freedom, but I will add them in due course and update the contribution of the sum of control noise to the best sensitivity.

Images attached to this comment