In case you do't see the plots press here: 14510.

Highlights

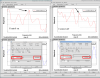
• I measured the decay times of 25 resonant modes with the control system on and off. The resonant frequencies were selected from measured force transfer functions and free swing displacement amplitude spectral densities (ASD).
• With the control system on the decay times of 24 modes are below 60 seconds. See first picture.
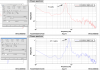
• The exception was the IP-L mode at 406 mHz: with the control system on the decay time is 35 seconds longer than with the control off. The corresponding data point is indicated by the arrow in the picture. This is likely due to injected noise because it was found that in the ASD the peak at such a frequency is 7% higher with the control on. See second picture.
• The first measurement for the IP-L mode at 406 mHz was done in a day with a relatively high microseismc condition but it was repeated when the micriseismic was low, yielding a similar result. Therefore, the seismic condition can be ruled out as the cause.

Highlights which are a byproduct of the measurements

• The resonant frequency in IP-L is not what was expected from previous measurments. It used to be 55 mHz, now it's 70 mHz. This was confirmed with transfer function measurments and the free swing spectra. This may be due to temperature change but more investigation is needed.
• Asymmetry was found in the IP: the resonant frequency in IP-T is different to the one in IP-L, namely, it's not at 70 mHz but at about 86 mHz according to free swing spectra with 5 mHz resolution. See third picture.
  • Maybe this would be a good chance to look for the craddle effect in the IP.
  • Depending on the plans for temperature control we might want to add more weight to the IP in order to reduce the resonant frequency.

Method

(Code referred to below is commented and the details can be found there.)

The envelope of the decaying oscilation was calculated using the Hilbert Transform in Matlab and then a decaying exponential was fitted to the envelope. In general, this method worked becuase in most of the cases the amplitude of other resonant modes present were not large enough to create a problem. The plots for each case can be seen by running the script indicated below. In some cases there were oscllations at lower frequencies whose amplitudes precent me frok using the same method. In those cases I used two approcches. One approach was to fit a sinusoidal fuction to the data and then substract the fitted curve to the data. This worked in two cases in which the sinusoidal fit was very good (BF at 226 mHz and 609 mHz with control on), but it failed when the fit wasn't good due to the presence of more modes (same modes with control off). In these more challenging cases I changed the method to calculate the envelope. The envelope was made to follow the higher frequency peaks and troughs only and the decaying amplitude was then characterized by the difference between the high and low envelopes. See fourth picture.

Directories and files

/kagra/Dropbox/Subsystems/VIS/TypeBData/SR2/quality_factors/

Experimental data

/kagra/Dropbox/Subsystems/VIS/TypeBData/SR2/quality_factors/decay_times/

Data files and scripts. The main script is decay_times_main.m

(Files haven't been moved to this location yet.)