[Sato (NAOJ), Kokeyama]
Measurment
Observation of the beam dump temperature of last day is attached. The maximum temperature was ~40 degC after ~9 hours with input beam of ~4W.
Plot was produced by GWData. See, /users/kokeyama/PEM_MON/HPBD_IFI.m
Results and discussions
Compared with a simple model (by NAOJ Sato-san, see below), the observed beam dump temperature is low, if we assume only the heat sinks, and is too high if we assum there is also the heat transfer on the SUS pedestals. It must be a mixture of the both, and also the radiation may be present.
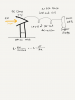
Sato-san's (NAOJ) thermal conduction model
Fourier's law on heat conduction is
q = -lambda * dT / dx
where q is the heat flux [W/m2], lambda is a thermal conductivity of the media, dT is the temperature difference between two points, dx is the distance between the two points.
Case 1. with only heat sinks,
- Heat flux: q = Input power [W] devided by a total cross section of the heat sinks [m2]. The input power was roughly 4W, and the cross section is 1.4e-5 x 10 as a cross section of one sink is 1.4e-5 m2, and 10 sinks are connected to the outer cupper flange.
- Thermal conductivity of cupper sink, lamda = 372 [W/m/K]
- Length of the heat sinks: dx = 0.75 [m]
- See also the second attached figure
Solveing this, dT is 58 degC. Assuming the room temperature is roughly 25 degC, the dump temperature is derived as 83 degC.
Case 2. with SUS pedestals,
- Heat flux: q = Input power [W] devided by a total cross section of the heat sinks [m2]. The input power was roughly 4W, and the cross section is 0.01m2 .
- Thermal conductivity of cupper sink, lamda = 16 [W/m/K]
- Length of the heat sinks: dx = 0.1 [m]
In this case, the expected dump temperature is 27 degC - even with much smaller thermal conductivity, this path conducts the heat more than the heat sinks.
The actual situation is the mixture of case 1 and 2. Akutsu-san suggested to fit the obtained data to get some realistic heat parameters. To be updated.